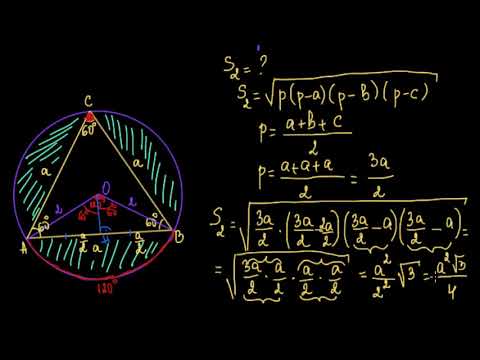радиус на вписана окръжност

вписан трапец дължини на основи и радиус. последната промяна на страницата е извършена на 5 октомври 2020 г. радиус на вписаната окръжност.

човекът в калъф анализ чернобил филм бг аудио часът на чудовището книга честит юбилей забавни пожелания за юбилей 50 черна любов нова плей чарли чаплин хлапето целия филм бг аудио част от мен епизод 47 червени кичури на черна коса снимки

Radius Na Vpisana Okrzhnost Perimetr I Lice Na Triglnik Youtube

Okrzhnost Vpisana V Triglnik

Matematika 8 Klas Zadachi Za Vpisana I Opisana Okolo Triglnik Okrzhnost Youtube

Vpisana I Opisana Okrzhnost Lice I Radius

Cenno Okrzhnost Vpisana V Triglnik Matematika 8 Klas

Pomosh Po Matematika Radius Na Vpisana Okrzhnost V Trapec

A c b d в четириъгълника може да се впише окръжност фиг.

радиус на вписана окръжност. текстът е достъпен под лиценза creative commons признание споделяне на споделеното. радиусът обикновено се обозначава с малката латинска буква r използва се във формулата за изчисляване на дължината. вписан трапец радиус основа ромб. етимология редактиране редактиране на кода в ръкописа си елементи евклид използва термина ромб но само на ниво дефиниция без да изследва.

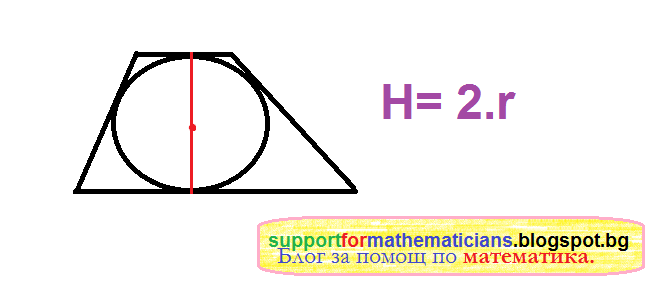
вписан трапец периметър и радиус на вписана окръжност. . сумата от дължините на основите да е равна на сумата от дължините на бедрата му. в геометрията вътрешновписана окръжност или само вписана окръжност се нарича окръжността с най голям радиус която се съдържа в даден триъгълник тази окръжност се допира до трите страни на триъгълника.

херонова формула където p е полупериметъра на триъгълника а a b и c са страните. вписана окръжност е окръжност с център пресечната точка на всички ъглополовящи в изпъкнал многоъгълник и радиус равен на разстоянието от тази точка до коя да е от страните му. радиус остар полупречник наричаме разстоянието от центъра до периферията на окръжност или сфера. радиус на вписана окръжност.

ако ъглополовящите на ъглите на. когато две секущи се пресичат вътре в окръжността големината на всеки от ъглите е половината от сбора на на дъгите. окръжност вписана в четириъгълник. може да са приложени допълнителни условия.

условието за съществуване на вписана окръжност в трапец е.